
World Cup 2019: Explaining why Pakistan have to win by a margin of 308 runs or more to qualify

There has been a lot of buzz around the World Cup 2019 knockout stages as although India, Australia and hosts England have made their way into the semi-finals, Pakistan still have a mathematical chance to make their way into the last four.
After England defeated New Zealand in the league stage on 3rd July, England claimed their spot into the final four along with Australia and India. New Zealand, on the other hand, were left to lament their poor show in the latter stages of the league stage as they succumbed to a massive 119-run against England.
With New Zealand's huge loss, their net run rate came crashing down to just +0.175 while Pakistan, prior to the game against Bangladesh started with a run rate of -0.792.
However, Sarfraz Ahmed's men could still find a spot in the semi-finals and here is how -
Here are some basics of the qualification scenario-
If Pakistan lose to Bangladesh -- New Zealand qualify directly.
If Pakistan beat Bangladesh - Net run rate will decide the winner.
How is the Net Run Rate calculated?
Run rate = (Runs scored by the team / balls taken to score) * 6
Net Run rate = ( (Runs scored in all matches / balls faced in all matches) - (Runs conceded in all matches/balls bowled in all matches) ) *6
On this note,
Final NRR of New Zealand -
(( 1674 / 2064 ) - (1868 / 2389 )) *6 = +0.1748.
NRR of Pakistan with one league match remaining against Bangladesh
(( 1710 / 2033) - ( 1773/ 1822)) *6 = -0.7919
From this, we see that New Zealand have a NRR of +0.1748 and Pakistan have -0.7919 with one more league match against Bangladesh.
In order to overthrow New Zealand and qualify for semis Pakistan should have a NRR of +0.1749 or above. We will formulate this mathematically,
Consider the equation to include the match against Bangladesh.
[( ( 1710 + U ) / (2033 + V )) - (( 1773 + X ) / ( 1822 + Y ))] * 6 >= 0.1749 -> (II)
Here, U = Runs to be scored by Pakistan against Bangladesh, V= Balls to be bowled by Bangladesh to Pakistan, X = Runs to be scored by Bangladesh against Pakistan, Y = Balls to be bowled by Pakistan to Bangladesh.
Now, let us consider two separate cases.
If Pakistan bat first against Bangladesh
In this case,
Either Pakistan are skittled out or bat throughout their quota of 50 overs. Hence, V = 300.
Assuming Pakistan win the match, Bangladesh are either all out in their 50 overs or play all 50 overs and do not reach the target. Hence, Y = 300.
Substituting the values of V and Y in the above equation and simplifying we get a magic equation which determines Pakistan's fate this World Cup.
Equation becomes -> 2122 * U - 2333 * X = 652099.
If we assume Bangladesh score 0, then X = 0 and U = 308. Hence, Pakistan have to score a minimum of 308 in their quota of 50 overs, else they are out of World Cup instantly.
If Pakistan manage 350, U = 350, Hence X = 38. Implies that Pakistan have to get Bangladesh all out for 38 runs or finish the quota of 50 overs. We extend the calculation and come to the following deductions.
Pakistan's qualification chances batting 1st ->
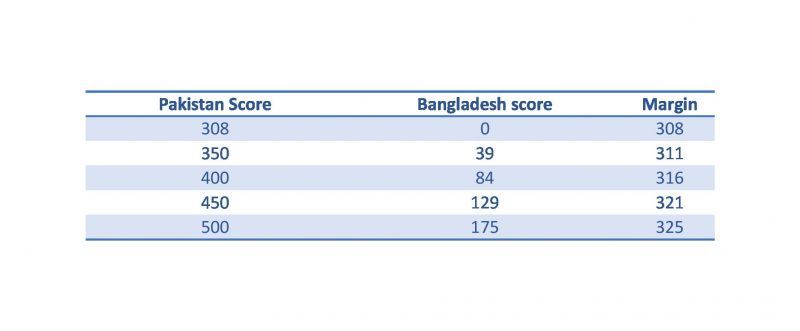
It almost looks improbable for Pakistan to win by such huge margin.
If Pakistan bat second against Bangladesh
Consider the equation (II) again.
Bangladesh either bat all their 50 overs or get all out. Hence, Y = 300.
Since Pakistan bat second , they can only lead Bangladesh by maximum of 7 runs up and above Bangladesh's score. This is a case if Pakistan smash a six on a no ball when the scores are tied. Hence, U = X+7.
Substituting the above values we get another equation which is handy for calculation.
Equation --> ( ( 1717 + X ) / 2033 + U ) - (1733 + X ) / 2122 ) * 6 ) = 0.02915.
Pakistan's chance to qualify batting 2nd ->
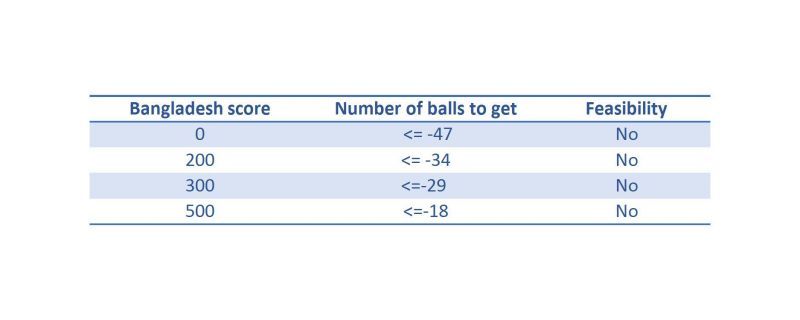
Thus, Pakistan does not fancy any chance of qualification given they bat second.